Aby dojść do ważnych, naukowych wniosków w dziedzinie astronomii nie trzeba wcale być wykwalifikowanym astronomem. Nie trzeba posiadać zaawansowanego sprzętu w postaci ogromnych, nowoczesnych teleskopów, ani nie trzeba angażować szeregu naukowców do opracowywania zebranych danych. I co istotne, nie trzeba też poświęcać na to zbyt wiele swojego, zapewne bardzo cennego czasu. Aby tego dokonać wystarczy wyjść w nocy na zewnątrz, spojrzeć w niebo, chwilę się zastanowić i zadać sobie proste pytanie: dlaczego niebo jest ciemne?
Artykuł przygotowała Marta Dziwer.
Odpowiedź na to pytanie może wydawać nam się teraz oczywista, jednak sformułowanie jej zajęło kolejnym pokoleniom uczonych ponad 400 lat. Nad ciemnością nocnego nieba zastanawiało się wielu czołowych astronomów jak Halley, fizyków – Kepler, Kelvin, kosmologów, a nawet poetów – np. Edgar Allan Poe. Jednak największą sławę temu problemowi zapewnił Wilhelm Heinrich Olbers, niemiecki lekarz i astronom, od którego nazwiska nazwano ów problem paradoksem Olbersa. Uczony ten w 1823 roku napisał jeden z rozdziałów Rocznika Obserwatorium Berlińskiego. Sformułował on wątpliwości swoich poprzedników, którymi byli: Digges, Kepler, Guericke, Halley i de Cheseaux w jednym pytaniu: „Dlaczego w nocy niebo jest ciemne, skoro patrząc w każdym kierunku patrzę na jakąś gwiazdę?”
To tak, jak wtedy, gdy stoimy w środku gęstego lasu: Między każdymi dwoma pniami, znajdzie się kolejny, także ostatecznie gdzie się nie popatrzymy, nasz wzrok zatrzymuje się na drzewie, bo ich liczba jest bardzo duża.
Według Olbersa tak samo powinno być z gwiazdami, skoro ich liczba jest nieskończona.
Ale czy liczba gwiazd na pewno jest nieskończona? Przecież niebo jest ciemne.
Cofnijmy się do czasów, w których panował model Wszechświata opisany przez Isaaca Newtona, czyli czasów, w których narodził się paradoks Olbersa. Bazując na oddziaływaniach grawitacyjnych, które sam opisał, Newton wywnioskował, że Wszechświat musi być nieskończony, inaczej cała materia znajdująca się w nim na wskutek ciążenia ku sobie, zbiłaby się w jednym miejscu. A więc mamy niepodważalny na miarę tamtych czasów fakt, że Wszechświat jest nieskończony.
Powtórzmy zatem rozumowanie Olbersa, które umieścił w swoim artykule ponad półtora wieku temu:
Po pierwsze: Wszechświat jest jednorodny w całej swej rozciągłości.
Po drugie: Wszechświat jest niezmienny w czasie.
Po trzecie: W przestrzeni kosmicznej nie występują ruchy o dużej skali.
I po czwarte: Prawa fizyki obowiązują w każdym miejscu.
Według modelu Newtona, Wszechświat jest nieskończony, jednorodny i statyczny. W takim modelu każdy punkt Wszechświata może być uważany za jego środek, zatem żaden nie jest w nim wyróżniony. Weźmy zatem punkt, w którym znajdujemy się my, nasza planeta, Ziemia. Przyjmijmy odpowiednio dużą skalę tak, żeby w jednostce objętości zaburzenia w rozmieszczeniu gwiazd przestały odgrywać jakiekolwiek znaczenie. Wokół tego punktu zatoczmy teraz dwie przestrzenie kuliste, mniejszą o promieniu r i większą o promieniu r + t. Dobierzmy je tak, żeby wartość r była znacząco większa od wartości t. Przyjmijmy dodatkowo M, jako średnią moc pojedynczej gwiazdy oraz N, jako liczbę gwiazd znajdujących się w przyjętej jednostce objętości.
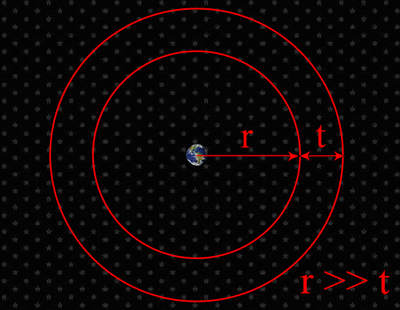
Wokół wybranego punktu zatoczmy dwie przestrzenie kuliste, mniejszą o promieniu r i większą o promieniu r + t. Dobierzmy je tak, żeby wartość r była znacząco większa od wartości t.
Objętość pomiędzy obiema zatoczonymi powierzchniami, pamiętając o tym, że r jest dużo większe niż t, wynosi 4πr2t. W niej znajduje się łącznie 4πr2tN gwiazd, a ich łączna moc promieniowania wynosi 4πr2tNM. Wiedząc, że natężenie promieniowania spada z kwadratem odległości, dochodzimy do tego, że z obszaru pomiędzy obiema zaznaczonymi powierzchniami do obserwatora na Ziemi w jednostce czasu dociera 4πtNM światła. Jak widać, ta liczba wcale nie zależy od promienia tej sfery. Jeśli więc tylko grubości dalszych warstw t, byłyby takie same, to z każdej z nich do obserwatora na Ziemi docierałaby taka sama ilość światła. To, co tracimy na natężeniu światła z pojedynczej gwiazdy, przez spadek natężenia z kwadratem odległości, rekompensuje nam wzrost (znów z kwadratem odległości) średniej liczby gwiazd w danej warstwie. Jeśli więc zakreślimy nieskończenie wiele warstw i dodamy natężenia promieniowania z nich, to, rozpatrując tę sytuację w nieskończonym Wszechświecie, otrzymamy sumę nieskończenie wielu identycznych wyrazów, różnych od zera. A więc będzie to wielkość nieskończona.
Zatem całe nasze niebo powinno być rozświetlone do jasności równej jasności poszczególnej gwiazdy, w każdym kierunku nasz wzrok powinien zatrzymywać się na jakiejś gwieździe.
A jednak, czego nie da się ukryć, tak nie jest. Dlaczego?
Ciąg dalszy można przeczytać Paradoks Olbersa, czyli dlaczego niebo jest ciemne? Część 2.„>tutaj.





