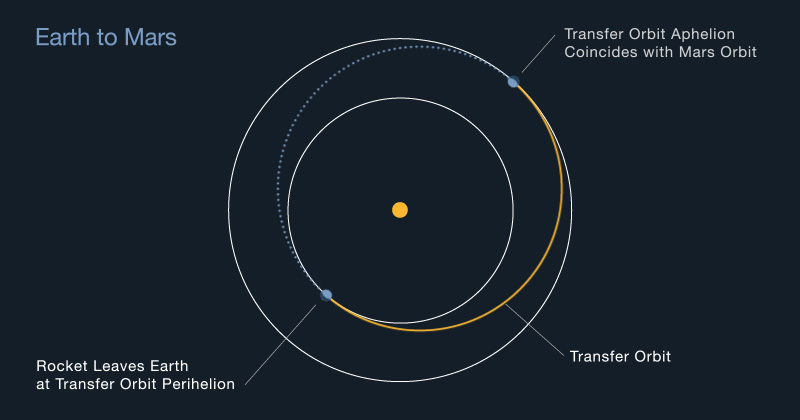
Z zagadnieniem trzech ciał (ang. Three-body problem) – i ogólniej n-ciał – astronomowie i fizycy zmagają się już od XVII wieku. Sformułował je sam Isaac Newton w słynnym „Philosophiae Naturalis Principia Mathematica”. Problem brzmi następująco: przy pomocy praw mechaniki klasycznej (zasad dynamiki Newtona i prawa powszechnego ciążenia) znaleźć trajektorię ruchu trzech ciał o skończonej masie przy zadanych warunkach początkowych (początkowych położeniach i prędkościach). Pomimo pracy wielu wybitnych naukowców (wśród nich Eulera, Lagrange’a czy Jacobiego!) nikomu nie udało się odnaleźć ogólnego wzoru opisującego trajektorie więcej niż dwóch ciał oddziałujących grawitacyjnie. Do dziś doczekaliśmy się jedynie rozwiązań numerycznych. Istnieją jednak rozwiązania charakteryzujące się pewnymi symetriami. Celem niniejszego artykułu jest próba przedstawienia kilku takich przykładów.
 Regular Keplerian motions in classical many-body systems, Eugene I Butikov, St Petersburg State University
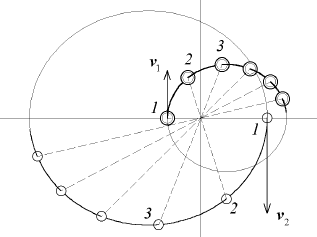
Regular Keplerian motions in classical many-body systems, Eugene I Butikov, St Petersburg State UniversityRys. 1: Tor ruchu dwóch ciał wokół środka masy układu, znajdującego się na przecięciu linii przerywanych.
Dlaczego to zagadnienie jest ważne? Ostatecznie można korzystać jedynie z rozwiązania problemu dwóch ciał tj. trajektorii wyznaczonych przez prawa Keplera dla danego układu. Trajektorie te będą krzywymi stożkowymi (np. elipsami, jak to przedstawiono na Rys. 1) o ogniskach w środku masy układu. Spodziewamy się bowiem, że np. wpływ oddziaływania grawitacyjnego Księżyca na orbity Ziemi i Słońca wokół ich wspólnego środka masy będzie znikomy ze względu na stosunkowo niewielką masę naszego naturalnego satelity. Tak samo pomijalny jest wpływ mało masywnych planet na tory ruchów gwiazd układów podwójnych. Czy jednak to samo można powiedzieć o oddziaływaniu grawitacyjnym Neptuna, Urana i Słońca? To właśnie teoretyczne obliczenia zaburzeń orbity Urana pozwoliły Le Verrierowi odkryć położenie ósmej planety Układu Słonecznego na sferze niebieskiej, co w konsekwencji doprowadziło do jej odkrycia w 1846 roku…
1. Przekonujemy się, iż jednym z najprostszych rozwiązań jest przypadek dwóch ciał o równych masach (np. planet o masach m1 = m2 = m) obiegających wspólny środek masy, w którym znajduje się ciało trzecie (np. gwiazda o masie M). Przyjmujemy, że w chwili t = 0 planety znajdowały się w równej odległości r od gwiazdy, a ich prędkości początkowe były równe co do modułu i kierunku ale przeciwne co do zwrotu. Ze względu na symetrię położeń planet spodziewamy się, iż gwiazda nie opuszcza środka masy. Ruch planet można zatem opisać ruchem w polu siły centralnej F o wartości odpowiednio zwiększonej przez oddziaływanie grawitacyjne gwiazdy:
Planety poruszają się po przystających krzywych stożkowych o ognisku w punkcie, w którym znajduje się gwiazda.
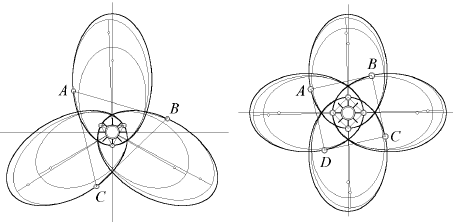
2. Możemy zastanowić się nad uogólnieniem przypadku nr 1. Przyjmijmy następujące ułożenie początkowe n identycznych planet i pojedynczej gwiazdy: w chwili t = 0 planety znajdują się w wierzchołkach n-kąta foremnego, ich prędkości początkowe są dobrane symetrycznie tj. mają jednakowe wartości i są skierowane są prostopadle do prostej łączącej je ze środkiem masy, zaś gwiazda jest w środku masy układu. Spodziewamy się, że gwiazda pozostanie w położeniu równowagi – tak jak w przykładzie pierwszym jest przyciągana przez każdą z planet z siłą o tej samej wartości. Ze względu na symetrię położeń planet oddziaływanie to znosi się. Rezultatem sumy sił grawitacyjnych n-1 planet i gwiazdy na jedną z nich jest siła centralna o zródle w punkcie położenia gwiazdy. Ponownie zatem spodziewamy się, iż orbita każdej z nich będzie krzywa stożkowa co przedstawia Rysunek 2 (odpowiednio 3 i 4 planety).
 Regular Keplerian motions in classical many-body systems, Eugene I Butikov, St Petersburg State University, St Petersburg, Russia
Regular Keplerian motions in classical many-body systems, Eugene I Butikov, St Petersburg State University, St Petersburg, RussiaRys. 2: Tor ruchu układu 3, 4 identycznych planet wokół wspólnego środka masy.
3. Co ciekawe, symetryczne ,,zachowywanie się” układu trzech ciał jest możliwe nawet w przypadku, w którym ciała te różnią się masami.
 Regular Keplerian motions in classical many-body systems, Eugene I Butikov, St Petersburg State University
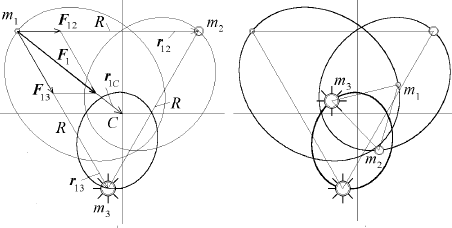
Regular Keplerian motions in classical many-body systems, Eugene I Butikov, St Petersburg State UniversityRys. 3: Stabilne orbity układu trzech ciał o różnych masach
Wystarczy, aby w chwili początkowej (t = 0) masy znajdowały się w wierzchołkach trójkąta równobocznego, zaś prędkość początkowa dla danego ciała była dobrana w taki sposób, aby suma sił oddziaływania grawitacyjnego dwóch pozostałych obiektów wyznaczała trajektorię eliptyczną o ognisku znajdującym się w środku masy układu. Nawet drobne odchylenie od tych warunków spowoduje zmianę położenia środka masy w przestrzeni w czasie, co skutkuje utratą stabilności orbit. Można bowiem udowodnić [1], że siła wywierana na jedno z ciał przez pozostałe dwie masy jest skierowana do środka masy. Warunek stabilności przestrzennej położenia środka masy zapewni zatem działanie siły centralnej i zwrotnie wyznaczy te same trajektorie ruchu (krzywe stożkowe), które były znalezione przy okazji wyznaczania prędkości początkowych.
Poszukiwanie nowych rozwiązań problemu trzech i n ciał jest nadal ciekawym zajęciem dla fizyków i astronomów. Ostatnich odkryć w tej dziedzinie dokonano w zeszłym roku! [2]
W świetle tych informacji, autorowi pozostaje tylko zachęcić Czytelnika do zgłębienia tego tematu.
- [1] Butikov, Eugene. (2000). Regular Keplerian motions in classical many-body systems. Eur. J. Phys. 21. 1-18. 10.1088/0143-0807/21/5/313
- [2] Li, Xiaoming; Liao, Shijun (2019). "Collisionless periodic orbits in the free-fall three-body problem". New Astronomy. 70: 22–26
- [3] The Three-Body Problem, Special Lecture: Wednesday October 11, 2006, Juhan Frank, LSU